【5. 智能优化算法案例】Matlab案例代码解析：智能优化算法篇

摩鑫产品

联系我们contact us

400-123-4657全国服务热线：

地址：: 广东省广州市天河区88号

邮箱：: admin@youweb.com

手机：: 13800000000

电话：: 400-123-4657

公司动态当前位置：首页 > 摩鑫动态 > 公司动态

【5. 智能优化算法案例】Matlab案例代码解析：智能优化算法篇添加时间：2024-07-22

记录于 2021-10-07。

差分进化算法（DE）
离散差分进化算法（DE）
差分进化算法实现指数拟合（DE-ExpFit）
梯度下降法曲线拟合（GradientDescent）
灰狼算法（GWO）
灰狼-布谷鸟算法（GWOCS）
粒子群算法（PSO）
离散粒子群算法（PSO）
粒子群算法实现指数拟合（PSO-ExpFit）
随机游走（RandWalk）
模拟退火算法实现指数拟合（SA）
模拟退火算法求解旅行商问题（SA-TSP）
樽海鞘算法（SSA）
状态转移算法（STA）
改进状态转移算法（STA）
鲸鱼算法（WOA）

基础篇：

https://zhuanlan.zhihu.com/p/408388753

Demo 篇：

https://zhuanlan.zhihu.com/p/409300387

基本流程：

初始化： $x_{ji,0}=rand*(x_j^U-x_J^L)+x_J^L$

变异： $v_{i,G+1}=x_{r1,G}+F*(x_{r2,G}-x_{r3,G}),F\\in{[0,2]}$

交叉： $u_{ji,G+1}=\\left\\{ \\begin{array}{l}v_{ji,G+1}&if &rand(j)\\leq{CR}&or &j=randi(i)\\\\ x_{ji,G+1}&if &rand(j)>{CR}&and &j\ eq{randi(i)}\\end{array}\\right.$

选择：试验值与当前目标值比较，实验值小则更新对应的种群值

边界处理：超过边界的可以用范围内随机值代替或者进行边界吸收直接用边界值代替

改进：

自适应差分进化算法： $\\lambda=e^{1-\\frac{G_m}{G_m+1-G}},F=F_0*2^{\\lambda}\\\\ CR=0.5*(1+rand)$

%%%%%%%%%%%%%  初始化 %%%%%%%%%%%%%
clear; clc;
% 种群数量
NP = 20;   
% 变量维度
D = 2;    
% 最大进化代数
G = 200;    
% 初始变异算子
F0 = 0.5;   
% 交叉算子
CR = 0.1;  
% 上限
Xs = 10; 
% 下限
Xx = -10;
% 阈值
yz = 1e-8;        
%%%%%%%%%%%%%  赋初值 %%%%%%%%%%%%%
Ob = zeros(NP, 1);
Ob1 = zeros(NP, 1);
% 变异种群
v = zeros(D, NP);   
% 选择种群
u = zeros(D, NP);  
% 初始种群
x = rand(D, NP) * (Xs - Xx) + Xx;  
%%%%%%%%%%%%%  计算目标函数 %%%%%%%%%%%%%
for m = 1 : NP
   Ob(m) = ObjFun(x(:, m));
end
%%%%%%%%%%%%%  差分进化循环 %%%%%%%%%%%%%
trace = zeros(G, 1);
trace(1) = min(Ob);
for gen = 1 : G
   %%%%%%%%%%%%%  变异操作 %%%%%%%%%%%%%
   %%%%%%%%%%%%%  自适应变异算子 %%%%%%%%%
   lamda = exp(1 - G / (G + 1 - gen));
   F = F0 * 2^lamda;
   %%%%%%%%%%  r1、r2、r3和m互不相同 %%%%%%%%%%
   for m = 1 : NP
      r1 = randi([1, NP], 1);
      while r1 == m
         r1 = randi([1, NP], 1);
      end
      r2 = randi([1, NP], 1);
      while r2 == m || r2 == r1
         r2 = randi([1, NP], 1);
      end
      r3 = randi([1, NP], 1);
      while r3 == m || r3 == r2 || r3 == r1
         r3 = randi([1, NP], 1);
      end
      v(:, m) = x(:, r1) + F*(x(:, r2) - x(:, r3));
   end
   %%%%%%%%%%%%%  交叉操作 %%%%%%%%%%%%%
   r = randi([1, D], 1);
   for n = 1 : D
      cr = rand;
      if cr <= CR || n == r
         u(n, :) = v(n, :);
      else
         u(n, :) = x(n, :);
      end
   end
   %%%%%%%%%%%%%  边界条件的处理 %%%%%%%%%%%%%
   for n = 1:D
      for m = 1:NP
         if u(n, m) < Xx || u(n, m) > Xs
            u(n, m) = rand*(Xs - Xx) + Xx;
         end
      end
   end
   %%%%%%%%%%%%%  边界吸收 %%%%%%%%%%%%%
%    for n=1 : D
%       for m=1 : NP
%          if u(n, m) < Xx
%             u(n, m)=Xx;
%          end
%          if u(n, m) > Xs
%             u(n, m)=Xs;
%          end
%       end
%    end
   %%%%%%%%%%%%%  选择操作 %%%%%%%%%%%%%
   for m = 1 : NP
      Ob1(m) = ObjFun(u(:, m));
   end
   for m = 1 : NP
      if Ob1(m) < Ob(m)
         x(:, m) = u(:, m);
      end
   end
   for m = 1:NP
      Ob(m) = ObjFun(x(:, m));
   end
   trace(gen + 1) = min(Ob);
   if min(Ob) < yz
      break;
   end
end
[SortOb, Index] = sort(Ob);
x = x(:, Index);
% 最优变量
X = x(:, 1); 
% 最优值
Y = min(Ob);        
disp(['最优x：' num2str(X')]);
disp(['最优y：' num2str(Y)]);
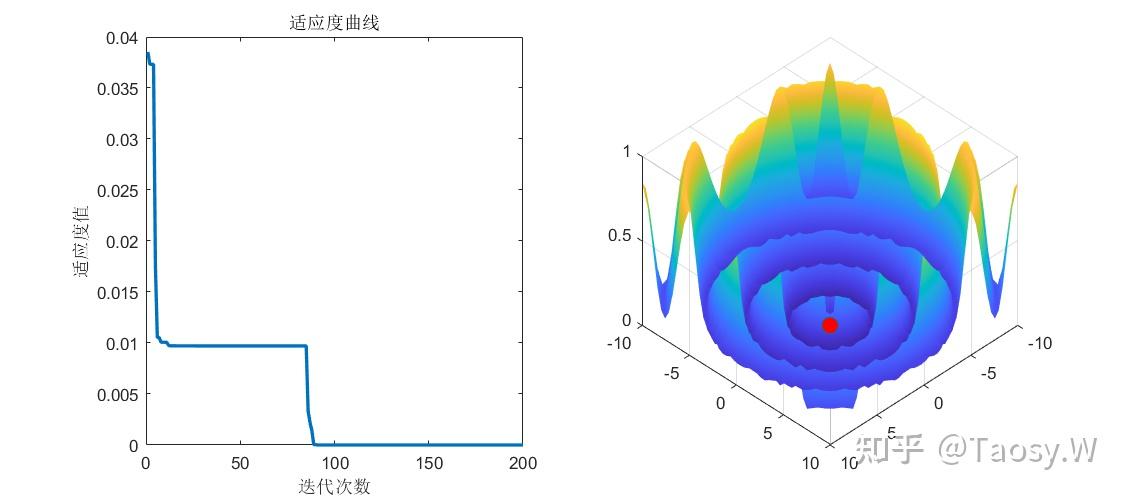
subplot(1, 2, 1)
plot(trace, 'LineWidth', 2);
xlabel('迭代次数');
ylabel('适应度值');
title('适应度进化曲线');
len = 50;
xRange = linspace(Xx, Xs, len);
yRange = linspace(Xx, Xs, len);
[xMap, yMap] = meshgrid(xRange, yRange);
zMap = zeros(len);
for i = 1 : len
    for j = 1 : len
        zMap(i, j) = ObjFun([xMap(i, j), yMap(i, j)]);
    end
end
subplot(1, 2, 2)
surf(xRange, yRange, zMap);
colorbar;
view(-45, -45);
shading interp
hold on
plot3(X(1), X(2), Y, 'o', 'MarkerFaceColor', 'r', 'MarkerSize', 10);
hold off
set(gcf, 'Position', [400, 200, 900, 400]);

function result = ObjFun(x)
x1 = x(1);
x2 = x(2);
t = x1^2 + x2^2;
result = 0.5 + (sin(sqrt(t))^2 - 0.5) / (1 + 0.001 * t)^2;
end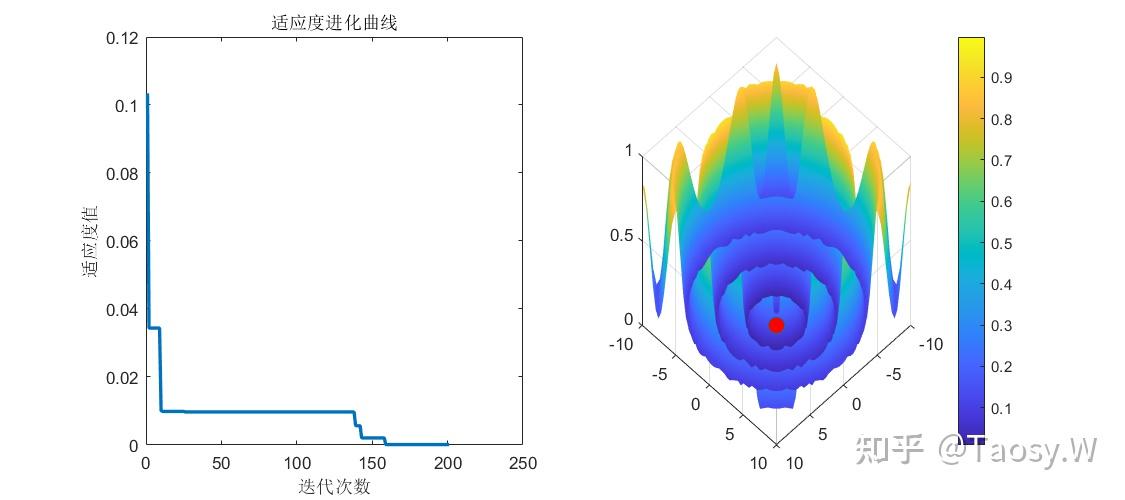

针对整数变量，用floor函数向下取整： $v_{i,G+1}=floor(x_{r1,G}+F*(x_{r2,G}-x_{r3,G}))$

%%%%%%%%%%%%%  离散差分进化算法求函数极值 %%%%%%%%%%%%%
%%%%%%%%%%%%%  初始化 %%%%%%%%%%%%%
clear;clc;
% 种群数量
NP = 20;   
% 变量维度
D = 2;       
% 最大进化代数
G = 200;      
% 初始编译算子
F = 0.5;     
% 交叉算子
CR = 0.1;  
% 上限
Xs = 100;  
% 下限
Xx = -100;                            
%%%%%%%%%%%%%  赋初值 %%%%%%%%%%%%%
Ob = zeros(NP, 1);
Ob1 = zeros(NP, 1);
trace = zeros(G + 1, 1);
% 变异种群
v = zeros(D, NP);  
% 选择种群
u = zeros(D, NP);    
% 初始种群
x = randi([Xx, Xs], D, NP);  
%%%%%%%%%%%%%  计算目标函数 %%%%%%%%%%%%%
for m = 1:NP
   Ob(m) = ObjFunInt(x(:, m));
end
trace(1) = min(Ob);
%%%%%%%%%%%%%  差分进化循环 %%%%%%%%%%%%%
for gen = 1:G
   %%%%%%%%%%%%%  变异操作 %%%%%%%%%%%%%
   %%%%%%%%%%  r1、r2、r3和m互不相同 %%%%%%%%%%
   for m = 1:NP
      r1 = randi([1, NP], 1);
      while r1 == m
         r1 = randi([1, NP], 1);
      end
      r2 = randi([1, NP], 1);
      while r2 == m || r2 == r1
         r2 = randi([1, NP], 1);
      end
      r3 = randi([1, NP], 1);
      while r3 == m || r3 == r2 || r3 == r1
         r3 = randi([1, NP], 1);
      end
      v(:, m) = floor(x(:, r1) + F*(x(:, r2) - x(:, r3)));
   end
   %%%%%%%%%%%%%  交叉操作 %%%%%%%%%%%%%
   r = randi([1, D], 1);
   for n = 1:D
      cr = rand;
      if cr <= CR || n == r
         u(n, :) = v(n, :);
      else
         u(n, :) = x(n, :);
      end
   end
   %%%%%%%%%%%%%  边界条件的处理 %%%%%%%%%%%%%
   %%%%%%%%%%%%%  边界吸收 %%%%%%%%%%%%%
   for n = 1:D
      for m = 1:NP
         if u(n, m) < Xx
            u(n, m) = Xx;
         end
         if u(n, m) > Xs
            u(n, m) = Xs;
         end
      end
   end
   %%%%%%%%%%%%%  选择操作 %%%%%%%%%%%%%
   for m = 1:NP
      Ob1(m) = ObjFunInt(u(:, m));
   end
   for m = 1:NP
      if Ob1(m) > Ob(m)
         x(:, m) = u(:, m);
      end
   end
   for m = 1:NP
      Ob(m) = ObjFunInt(x(:, m));
   end
   trace(gen + 1) = min(Ob);
end
[SortOb, Index] = sort(Ob);
x = x(:, Index);
% 最优变量
X = x(:, 1);   
% 最优值
Y = min(Ob);                 
disp(['最优x：' num2str(X')]);
disp(['最优y：' num2str(Y)]);
subplot(1, 2, 1)
plot(trace, 'LineWidth', 2);
xlabel('迭代次数');
ylabel('适应度值');
title('适应度进化曲线');
len = 200;
xRange = linspace(Xx, Xs, len);
yRange = linspace(Xx, Xs, len);
[xMap, yMap] = meshgrid(xRange, yRange);
zMap = zeros(len);
for i = 1 : len
    for j = 1 : len
        zMap(i, j) = ObjFunInt([xMap(i, j), yMap(i, j)]);
    end
end
subplot(1, 2, 2)
surf(xRange, yRange, zMap);
colorbar;
view(-45, 45);
shading interp
hold on
plot3(X(1), X(2), Y, 'o', 'MarkerFaceColor', 'r', 'MarkerSize', 10);
hold off
set(gcf, 'Position', [400, 200, 900, 400]);

function result = ObjFunInt(x)
result = -((x(1).^2 + x(2) - 1).^2 + (x(1) + x(2).^2 - 7).^2)/200 + 10;
end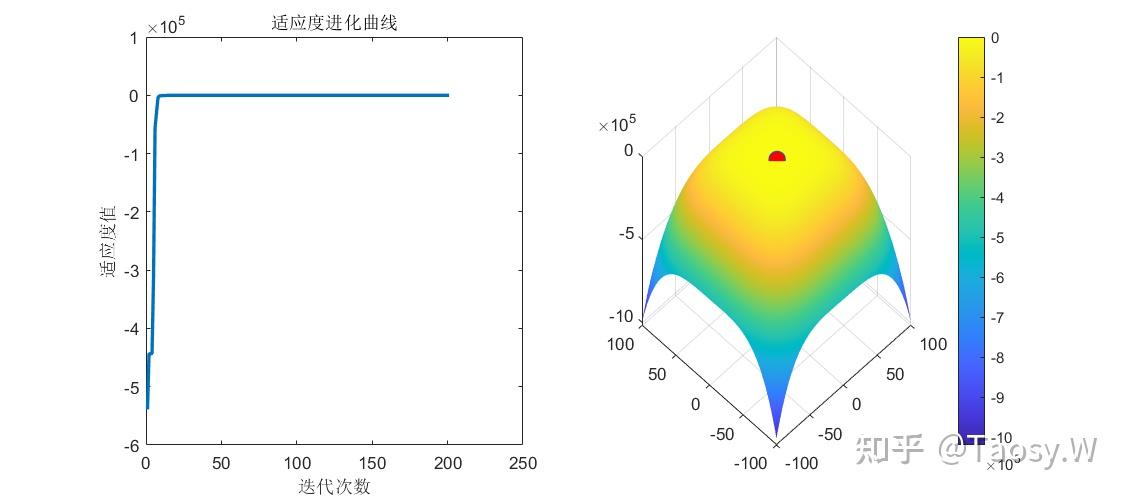

clear;clc;
t = 0.2*(1:3000)';
data = 400*exp(-t/5) + 10*randn(size(t));
tic;
p = DE_ExpFit(t, data)
toc;
fit = p(1)*exp(-t/p(2)) + p(3);
plot(t, data, t, fit, 'LineWidth', 2)
legend('model', 'DE');
title('差分进化算法实现指数拟合');

function [x_opt, y_opt]= DE_ExpFit(t, Et)
%{
函数功能：差分进化算法实现指数拟合：y=a*exp(-x/b) + c
输入：
  t：自变量；
  Et：因变量；
输出：
  x_opt：最优解；
  y_opt：适应度（目标函数值）；
%} 
% 初始值
NP = 50;                          % 种群数量
D = 3;                            % 变量维度
G = 200;                          % 最大进化代数
F0 = 0.5;                         % 初始变异算子
CR = 0.9;                         % 交叉算子
max_sig = max(Et);
Xmin = [0.5*max_sig, -2, 0];           % 下限
Xmax = [1.5*max_sig, 4, 0.5*max_sig];  % 上限；
%%%%%%%%%%%%%  赋初值 %%%%%%%%%%%%%
Ob = zeros(NP, 1);
Ob1 = zeros(NP, 1);
v = zeros(NP, D);                    % 变异种群
u = zeros(NP, D);                    % 选择种群
x = rand(NP, D).*repmat(Xmax - Xmin, NP, 1) + repmat(Xmin, NP, 1);
%%%%%%%%%%%%%  计算目标函数 %%%%%%%%%%%%%
for m = 1 : NP
    Ob(m) = Obj_Fit(x(m, :), t, Et);
end
y_opt = zeros(1, G);
%%%%%%%%%%%%%  差分进化循环 %%%%%%%%%%%%%
for gen = 1 : G
    %%%%%%%%%%%%%  变异操作 %%%%%%%%%%%%%
    %%%%%%%%%%%%%  自适应变异算子 %%%%%%%%%
    lamda = exp(1 - G/(G + 1 - gen));
    F = F0*2^lamda;
    %%%%%%%%%%  r1、r2、r3和m互不相同 %%%%%%%%%%
    for m = 1 : NP
        r1 = randi([1, NP], 1);
        while r1 == m
            r1 = randi([1, NP], 1);
        end
        r2 = randi([1, NP], 1);
        while r2 == m || r2 == r1
            r2 = randi([1, NP], 1);
        end
        r3 = randi([1, NP], 1);
        while r3 == m || r3 == r2 || r3 == r1
            r3 = randi([1, NP], 1);
        end
        v(m, :) = x(r1, :) + F*(x(r2, :) - x(r3, :));
    end
    %%%%%%%%%%%%%  交叉操作 %%%%%%%%%%%%%
    r = randi([1, D], 1);
    for n = 1:D
        cr = rand;
        if cr <= CR || n == r
            u(:, n) = v(:, n);
        else
            u(:, n) = x(:, n);
        end
    end
    %%%%%%%%%%%%%  边界条件的处理 %%%%%%%%%%%%%
    % ①范围内随机值
       for n = 1:NP
          for m = 1:D
             if u(n, m) < Xmin(m) || u(n, m) > Xmax(m)
                u(n, m) = rand*(Xmax(m) - Xmin(m)) + Xmin(m);
             end
          end
       end
    % ②边界吸收
%     for n=1 : NP
%         for m=1 : D
%             if u(n, m) < Xmin(m)
%                 u(n, m)=Xmin(m);
%             end
%             if u(n, m) > Xmax(m)
%                 u(n, m)=Xmax(m);
%             end
%         end
%     end
    %%%%%%%%%%%%%  选择操作 %%%%%%%%%%%%%
    for m = 1 : NP
        Ob1(m) = Obj_Fit(u(m, :), t, Et);
    end
    for m = 1 : NP
        if Ob1(m) < Ob(m)
            x(m, :) = u(m, :);
        end
    end
    for m = 1 : NP
        Ob(m) = Obj_Fit(x(m, :), t, Et);
    end
    y_opt(gen) = min(Ob);
end
[~, Index] = min(Ob);
x_opt = x(Index, :);
x_opt(2) = 10^(x_opt(2));
end

% 目标函数
function fitError = Obj_Fit(p0, t ,Et)
A = p0(1);
B = p0(2);
C = p0(3);
f = A*exp(-t/10^B)  + C;  
fitError = norm(Et - f);
end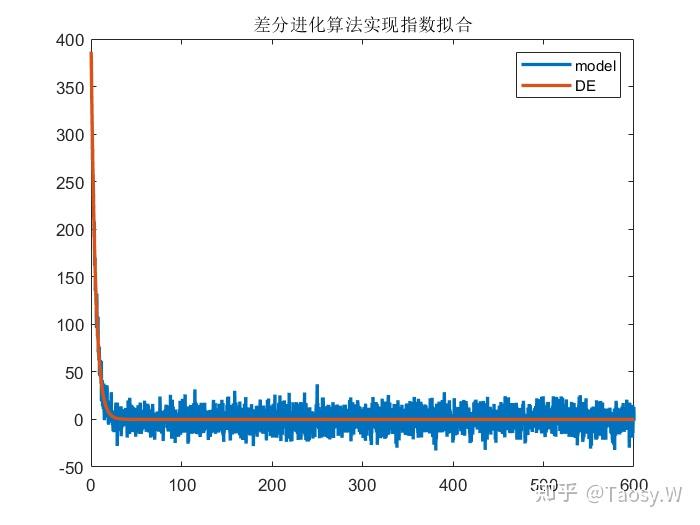

clear; clc;
t = [ 0.1350, 0.2600, 0.3800, 0.5050, 0.6450, 0.8100, 1.0000, 1.2150, 1.4600, 1.7400, 2.0550, 2.4150, ...
       2.8150, 3.2650, 3.7650, 4.3200, 4.9350, 5.6100, 6.3450, 7.1500, 8.0200, 8.9650, 9.9800, 11.0650, ...
       12.2200, 13.4500, 14.7500, 16.1150, 17.5450, 19.0400, 20.5950, 22.1950, 23.8450, 25.5350, ...
       27.2600, 29.2650, 32.2700, 36.2800, 41.4850, 47.8900, 55.8950, 65.5000, 77.5050, 92.3100, ...
      108.7150, 128.3250, 151.9300, 179.9350, 212.9400, 252.9450]';
M = length(t);
% 构造模型
A =1800;
B = 15;
qMrl = 5;
AA = 50;
C = 10;
rng('default');
ratio = 0;
noise = ratio * randn(M, 1);
Et = A * exp(-t / B - 0.5 * qMrl * t.^2) + AA * exp(-t / B) + C + noise;
% 梯度下降法学习
% 初始参数
alpha = 1;   % 学习率大收敛快，可能有震荡
iteMax = 1000000;
iniA = 1;
iniB = rand;
iniQMrl = rand;
iniAA = rand;
iniC = rand;
initW = [iniA; iniB; iniQMrl; iniAA; iniC];
err = 1e-6;
J = zeros(iteMax, 1);
G = zeros(size(initW));
e = 0.1;
convIter = 0;
for i = 1 : iteMax
    gradA = 2 * iniA * exp(- 0.5 * iniQMrl^2 * t.^2 - t / iniB^2);
    gradB = (2 * iniA^2 * t .* exp(-0.5 * iniQMrl^2 * t.^2 - t / iniB^2)) / iniB^3 + (2 * iniAA^2 * t .* exp(-t /iniB^2)) / iniB^3;
    gradQMrl = - iniA^2 * iniQMrl * t.^2 .* exp(-0.5 * iniQMrl^2 * t.^2 - t / iniB^2);
    gradAA = 2 * iniAA * exp(-t / iniB^2);
    gradC = 2 * iniC * ones(M, 1);
    grad = 1 / M * [gradA, gradB, gradQMrl, gradAA, gradC]' * (iniA^2 * exp(-t / iniB^2 - 0.5 * iniQMrl^2 * t.^2) + iniAA^2 * exp(-t / iniB^2) + iniC^2 - Et);
    % Adagrad 法    x=x + yita * inv(G) * grad;
    G = G + grad.^2;
    newW = initW - alpha * diag(1 https://zhuanlan.zhihu.com/p/ sqrt(G + e)) * grad;
%     newW=initW - alpha * grad;
    if max(abs((newW - initW))) < err
        convIter = convIter + 1;
        if convIter == 10
            J(i + 1 : end) = [];
            disp(['梯度下降法迭代次数：', num2str(i)]);
            result = newW';
            result(1) = newW(1)^2;
            result(2) = newW(2)^2;
            result(3) = newW(3)^2;
            result(4) = newW(4)^2;
            result(5) = newW(5)^2;
            disp(['梯度下降法迭代结果：', num2str(result)]);
            break;
        end  
    else
        convIter = 0;
        initW = newW;
        iniA = newW(1);
        iniB = newW(2);
        iniQMrl = newW(3);
        iniAA = newW(4);
        iniC = newW(5);
        J(i) = 1 / (2 * M) * norm(iniA^2 * exp(-t / iniB^2 - 0.5 * iniQMrl^2 * t.^2) + iniAA^2 * exp(-t / iniB^2) + iniC^2 - Et)^2;
    end
end
fit = iniA^2 * exp(-t / iniB^2 - 0.5 * iniQMrl^2 * t.^2) + iniAA^2 * exp(-t / iniB^2) + iniC^2;
% 绘图
figure('Position', [50, 50, 900, 400]);
subplot(1, 2, 1)
loglog(J, 'LineWidth', 2)
legend(['alpha=', num2str(alpha)]);
subplot(1, 2, 2)
semilogx(t, Et, 'ok', 'MarkerFaceColor', 'r', 'MarkerSIze', 5, 'LineWidth', 1.5)
hold on
plot(t, fit, 'LineWidth', 1.5)
hold off
legend('Model', 'Fitting')
title('梯度下降法曲线拟合');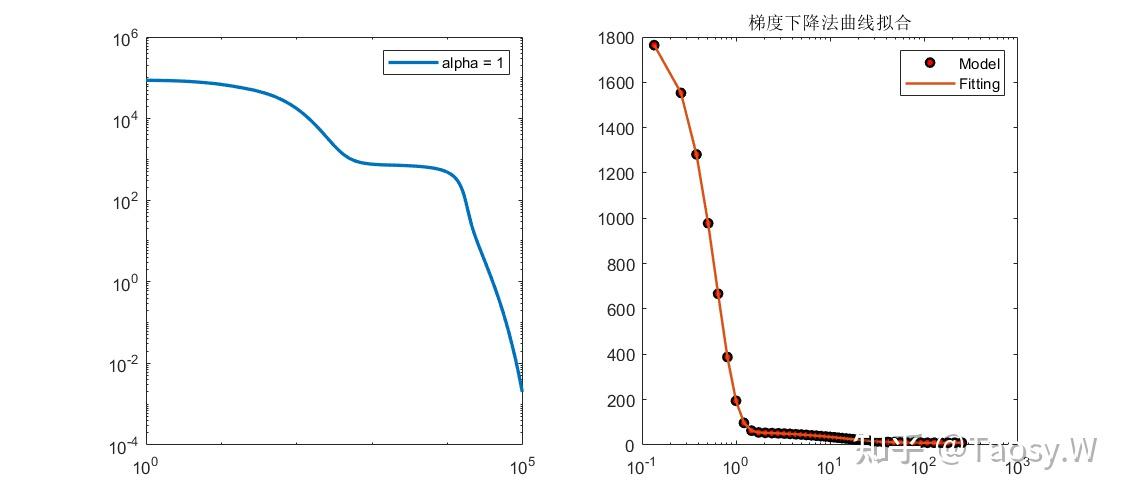

https://zhuanlan.zhihu.com/p/416365776 https://zhuanlan.zhihu.com/p/416365776 https://zhuanlan.zhihu.com/p/365689519

粒子状态更新

$s(v_{ij})=\\frac{1}{1+exp(-v_{ij})}\\\\ \\left\\{ \\begin{array}{l}1,&rand<s(v_{ij})\\\\ 0,&other \\end{array}\\right.$

clear;clc;
% 群体例子个数
N = 100; 
% 粒子维度
D = 20;             
T = 200;            % 最大迭代次数
c1 = 1.5;           % 学习因子1  
c2 = 1.5;           % 学习因子2
wMax = 0.8;         % 惯性权重最大值
wMin = 0.4;         % 惯性权重最小值
xMax = 10;          % 位置最大值
xMin =  -10;        % 位置最小值
vMax = 10;          % 速度最大值
vMin = -10;         % 速度最小值
%%%%%%%%%%  初始化种群个体（限定位置和速度） %%%%%%%%%
% 随机获得二进制编码的初始种群
x = randi([0, 1], N, D);   
v = rand(N, D) * (vMax - vMin) + vMin;
%%%%%%%%%%  初始化个体最优位置和最优值 %%%%%%%%%
p = x;
pbest = ones(N, 1);
for i = 1:N
   pbest(i) = ObjFunDiscrete(x(i, :), xMax, xMin);
end
%%%%%%%%%%  初始化全局最优位置和最优值 %%%%%%%%%
g = ones(1, D);
gbest = inf;
for i = 1:N
   if pbest(i) < gbest
      g = p(i, :);
      gbest = pbest(i);
   end
end
gb = ones(1, T);
vx = zeros(N, D);
%%%%%%%%%%  按照公式依次迭代直到满足精度或者迭代次数 %%%%%%%%%
for i = 1:T
   for j = 1:N
      %%%%%%%%%%  更新个体最优位置和最优值 %%%%%%%%%
      if ObjFunDiscrete(x(j, :), xMax, xMin) < pbest(j)
         p(j, :) = x(j, :);
         pbest(j) = ObjFunDiscrete(x(j, :), xMax, xMin);
      end
      %%%%%%%%%%  更新全局最优位置和最优值 %%%%%%%%%
      if pbest(j) < gbest
         g = p(j, :);
         gbest = pbest(j);
      end
      %%%%%%%%%%  动态计算惯性权重值 %%%%%%%%%
      w = wMax - (wMax - wMin) * i / T;
      %%%%%%%%%%  更新位置和速度值 %%%%%%%%%
      v(j, :) = w * v(j, :) + c1 * rand * (p(j, :) - x(j, :)) + c2 * rand * (g - x(j, :));
      x(j, :) = x(j, :) + v(j, :);
      %%%%%%%%%%  边界条件处理 %%%%%%%%%
      for ii = 1:D
         if (v(j, ii) > vMax) || (v(j, ii) < vMin)
            v(j, ii) = rand * (vMax - vMin) + vMin;
         end
      end
      vx(j, :) = 1 https://zhuanlan.zhihu.com/p/ (1 + exp(-v(j, :)));
      for jj = 1 : D
         if vx(j, jj) > rand
            x(j, jj) = 1;
         else
            x(j, jj) = 0;
         end
      end
   end
      %%%%%%%%%%  记录历代全局最优值 %%%%%%%%%
      gb(i) = gbest;
end
m = 0;
for j = 1:D
   m = m + g(j) * 2^(j - 1);
end
f1 = xMin + m * (xMax - xMin)/(2^D - 1);
disp(['最优个体：' num2str(f1)]);
disp(['最优值：' num2str(gb(end))]);
subplot(1, 2, 1);
plot(gb, 'LineWidth', 2);
xlabel('迭代次数');
ylabel('适应度值');
title('适应度进化曲线');
subplot(1, 2, 2)
xRange = linspace(xMin, xMax, 100);
yRange = xRange + 6 * sin(4 * xRange) + 9 * cos(5 * xRange);
plot(xRange, yRange, 'LineWidth', 2);
hold on;
plot(f1, gb(end),'o', 'MarkerFaceColor', 'r', 'MarkerSize', 10);
hold off;
set(gcf, 'Position', [400, 200, 900, 400]);

function result = ObjFunDiscrete(x, xMax, xMin)
%%%%%%%%%%  适应度函数  %%%%%%%%%%%
m = 0;
D = length(x);
for j = 1:D
   m = m + x(j) * 2^(j - 1);
end
% 译码成十进制数
f = xMin + m * (xMax - xMin) / (2^D - 1);    
fit = f + 6 * sin(4 * f) + 9 * cos(5 * f);
result = fit;
end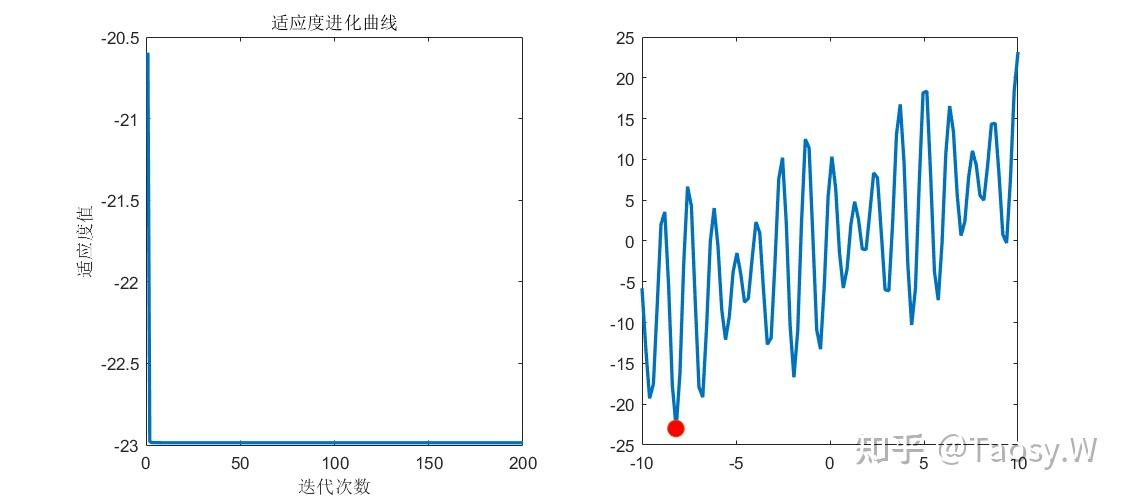

粒子群算法实现指数拟合（PSO-ExpFit）

clear;clc;
t = 0.2*(1:3000)';
data = 400*exp(-t/5) + 10*randn(size(t));
tic;
p = PSO_ExpFit(t, data)
toc;
fit = p(1)*exp(-t/p(2)) + p(3);
plot(t, data, t, fit, 'LineWidth', 2)
legend('model', 'PSO');
title('压缩因子粒子群算法实现指数拟合');

function [x_opt, y_opt]= PSO_ExpFit(t, Et)
%{
函数功能：压缩因子粒子群算法实现指数拟合：y=a*exp(-x/b) + c
输入：
  t：自变量；
  Et：因变量；
输出：
  x_opt：最优解；
  y_opt：适应度（目标函数值）；
%} 
% 初始值
D = 3;                % 粒子维度，未知数个数；
IterMax = 200;        % 最大迭代次数；
Vmin = -1;            % 速度最小值；
Vmax = 1;             % 速度最大值；
c1 = 2.05;            % 学习因子1，认知部分；
c2 = 2.05;            % 学习因子2，社会部分；
N = 200;              % 种群个数；
max_sig = max(Et);
Xmin = [0.5*max_sig, -2, 0];    % 下限
Xmax = [1.5*max_sig, 4, 0.5*max_sig];  % 上限；
% 计算
phy = c1 + c2;
lamda = 2 / abs(2 - phy - sqrt(phy^2 - 4*phy));   % 压缩因子
% 初始化种群个体（限定位置和速度） 
x = rand(N, D).*repmat(Xmax - Xmin, N, 1) + repmat(Xmin, N, 1);
v = rand(N, D)*(Vmax - Vmin) + Vmin;
% 初始化个体最优位置和最优值 
p = x;
pbest = ones(1, N);
for i = 1 : N
   pbest(i) = Obj_Fit(x(i, :), t ,Et);
end
% 初始化全局最优位置和最优值 
g = ones(1, D);
gbest = inf;
for i = 1 : N
   if pbest(i) < gbest
      g = p(i, :);
      gbest = pbest(i);
   end
end
% 迭代直到满足精度或者迭代次数 
fx = zeros(1, N);
y_opt = zeros(1, IterMax);
for i = 1 : IterMax
   for j = 1 : N
      % 更新个体最优位置和最优值 
      fx(j) = Obj_Fit(x(j, :), t ,Et);
      if fx(j) < pbest(j)
         p(j, :) = x(j, :);
         pbest(j) = fx(j);
      end
      % 更新全局最优位置和最优值 
      if pbest(j) < gbest
         g = p(j, :);
         gbest = pbest(j);
      end
      % 更新位置和速度值  
      v(j, :) = lamda*v(j, :) + c1*rand*(p(j, :) - x(j, :)) + c2*rand*(g - x(j, :));
      x(j, :) = x(j, :) + v(j, :);
      % 边界条件处理 
      for ii = 1 : D
         if (v(j, ii) > Vmax) || (v(j, ii) < Vmin)
            v(j, ii) = rand*(Vmax - Vmin) + Vmin;
         end
         if (x(j, ii) > Xmax(ii)) || (x(j, ii) < Xmin(ii))
            x(j, ii) = rand*(Xmax(ii) - Xmin(ii)) + Xmin(ii);
         end
      end
   end
end
x_opt = g;
x_opt(2) = 10^(x_opt(2));
end

% 目标函数
function fitError = Obj_Fit(p0, t ,Et)
A = p0(1);
B = p0(2);
C = p0(3);
f = A*exp(-t/10^B)  + C;  
fitError = norm(Et - f);
end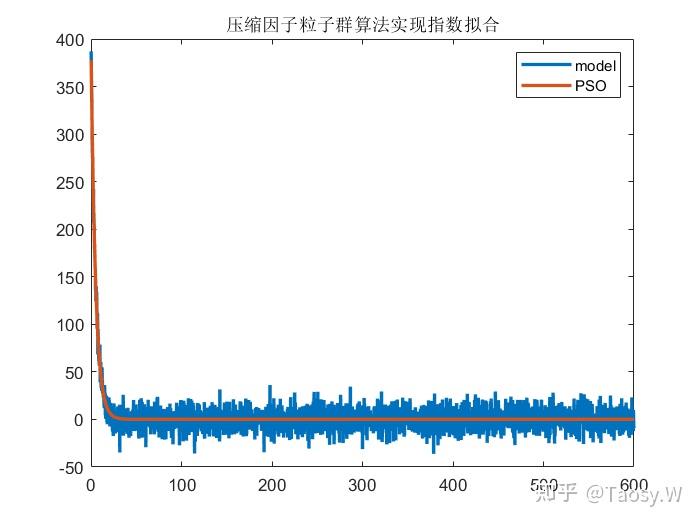

clear;clc;
lb = [-10, -10];
ub = [10, 10];
x0 = rand(1, 2) .* (ub - lb) + lb;
rng('default');
[mx, minf] = OptRandWalk(x0, 10, 100, 10);
disp(['最优值：' num2str(mx)]);
disp(['最优值对应目标函数：' num2str(minf)]);
len = 100;
xRange = linspace(-10, 10, len);
yRange = linspace(-10, 10, len);
[xMap, yMap] = meshgrid(xRange, yRange);
zMap = zeros(len);
for i = 1 : len
    for j = 1 : len
        zMap(i, j) = func([xMap(i, j), yMap(i, j)]);
    end
end
surf(xRange, yRange, zMap);
view(-45, -45);
shading interp
hold on
plot3(mx(1), mx(2), minf, 'o', 'MarkerFaceColor', 'r', 'MarkerSize', 10);
hold off
title('随机行走法求函数的极小值');

function[mx, minf]= OptRandWalk(x, lamda, N, n)
%{ 
函数功能：随机行走法求函数的极小值
x：初始值；
lamda：步长；
N：为了产生较好点的迭代次数；
n：单步循环行走次数，目的是尽可能走到全局最优点附近
mx：最优解；
minf：最优值。
%}
F = zeros(n, 1);
D = length(x);
X = zeros(n, D);
epsilon = 1e-6;
f1 = func(x);
while lamda  >= epsilon
    k = 1;
    while(k <= N)
        u = 2*rand(n, D) - 1;
        for ii =1 : n
            X(ii, :) = x + lamda*(u(ii, :) / norm(u(ii, :)));
            F(ii) = func(X(ii, :));
        end
        [f11, kk] = min(F);
        if f11 < f1
            f1 = f11;
            x = X(kk, :);
            k = 1;
        else
            k = k + 1;
        end
    end
lamda = lamda / 2;
end
mx = X(kk, :);
minf = f1;
end


function f = func(x)
% f=-sin(sqrt((x(1) - 100).^2 + (x(2) - 100).^2 ) + exp(1)) https://zhuanlan.zhihu.com/p/ (sqrt((x(1) - 100).^2 + (x(2) - 100).^2 ) + exp(1)) - 1;
% f=sum(x.^2);
% f=3*cos(x(1)*x(2)) + x(1) + x(2)^2;
% f=4*x(1)^2-2.1*x(1)^4+x(1)^6/3+x(1)*x(2)-4*x(2)^2+4*x(2)^4;
% f=0.5 + (sin(sqrt(x(1)^2 + x(2)^2))^2 - 0.5) / (1 + 0.001*(x(1)^2 + x(2)^2))^2;
x1 = x(1);
x2 = x(2);
t = x1^2 + x2^2;
f = 0.5 + (sin(sqrt(t))^2 - 0.5) / (1 + 0.001 * t)^2;
end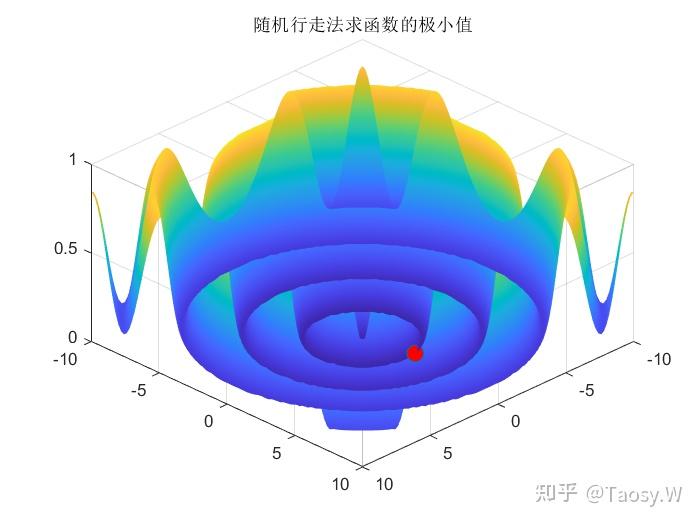

clear;clc;
t = 0.2*(1:3000)';
data = 400*exp(-t/5) + 10*randn(size(t));
tic;
p = SAA_ExpFit(t, data)
toc;
fit = p(1)*exp(-t/p(2)) + p(3);
plot(t, data, t, fit, 'LineWidth', 2)
legend('model', 'SA');
title('模拟退火算法实现指数拟合');

function p0 = SAA_ExpFit(t, Et)
%{
函数功能：模拟退火算法实现指数拟合：y=a*exp(-x/b) + c
输入：
  t：自变量；
  Et：因变量；
输出：
  x_opt：最优解；
  y_opt：适应度（目标函数值）；
%}   
% initial condition
T0= 1000;     % initial temperature
alpha= 0.99;  % annealing factor
N_max= 3000;  % max iterations
% range of varibles
max_sig = max(Et);
Xmin = [0.5*max_sig, -2, 0];           % 下限
Xmax = [1.5*max_sig, 4, 0.5*max_sig];  % 上限；
% initial value
var = rand(1,3).*(Xmax - Xmin) + Xmin;
fun = Obj_Fit(var, t, Et);
% iterative
for i= 1:N_max
  Tk= T0*alpha^(i-1);
    dvar = Tk*sign(rand(1,3)-0.5).*((1+1/Tk).^abs(2*rand(1,3)-1)-1);
    var1 = var + dvar.*(Xmax - Xmin);
    % accept it or not
    if all(var1 >= Xmin) && all(var1 <= Xmax)
      new_fun = Obj_Fit(var1, t, Et);
      if (new_fun <= fun) 
        var = var1;
        fun = new_fun;
      else
        if exp(-(new_fun-fun)/Tk)>rand
          var = var1;
          fun = new_fun;
        end
      end
    end
end
% results
p0 = [var(1), 10^var(2), var(3)]'; 
end


function fitError = Obj_Fit(p0, t ,Et)
A1 = p0(1);
B1 = p0(2);
A0 = p0(3);
f = A1*exp(-t/10^(B1 + eps)) + A0;  
fitError = norm(Et - f);
end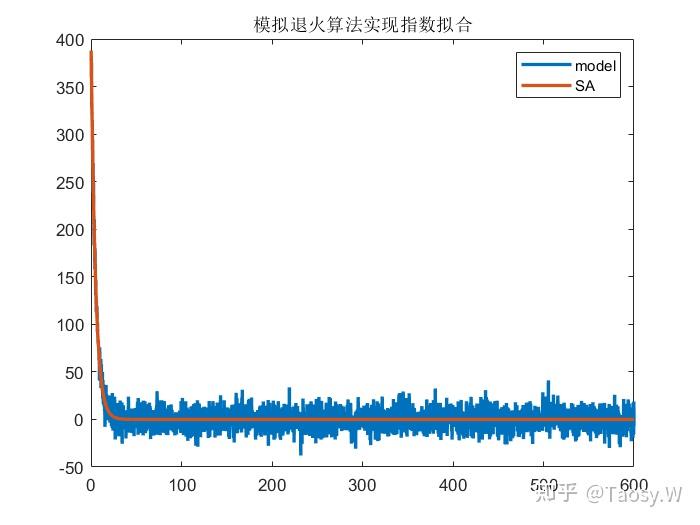

clear;clc;
ratio = 0.99;	    
t_start = 100; 
t_end = 1;        
Markov_length = 5000;	
coordinates = load('CityCoordinates.txt');
amount = size(coordinates, 1); 	% 城市的数目
% 通过向量化的方法计算距离矩阵
coor_x_tmp1 = coordinates(:,1) * ones(1, amount);
coor_x_tmp2 = coor_x_tmp1';
coor_y_tmp1 = coordinates(:, 2) * ones(1, amount);
coor_y_tmp2 = coor_y_tmp1';
dist_matrix = sqrt((coor_x_tmp1 - coor_x_tmp2).^2 + (coor_y_tmp1 - coor_y_tmp2).^2);
sol_new = 1 : amount;         % 产生初始解
% sol_new 是每次产生的新解；
% sol_current 是当前解；
% sol_best 是冷却中的最好解；
% E_current 是当前解对应的回路距离；
% E_new 是新解的回路距离；
% E_best 是最优解的
E_current = inf;        
E_best = inf; 		
sol_current = sol_new; 
sol_best = sol_new;
t = t_start;          
while t >= t_end
    % 当前温度下循环
    for r = 1 : Markov_length		
        % 产生随机扰动
        if (rand < 0.5)	% 随机决定是进行两交换还是三交换
            % 两交换
            ind = randperm(amount, 2);
            ind1 = ind(1);
            ind2 = ind(2);            
            tmp1 = sol_new(ind1);
            sol_new(ind1) = sol_new(ind2);
            sol_new(ind2) = tmp1;
        else
            % 三交换
            ind = randperm(amount, 3);
            % 确保ind1 < ind2 < ind3
            ind = sort(ind);
            ind1 = ind(1);
            ind2 = ind(2);
            ind3 = ind(3);
            tmplist1 = sol_new(ind1 + 1 : ind2 - 1);
            sol_new(ind1 + 1 : ind1 + ind3 - ind2 + 1) = sol_new(ind2 : ind3);
            sol_new(ind1 + ind3 - ind2 + 2 : ind3) = tmplist1;
        end       
        % 计算目标函数值
        E_new = 0;
        for i = 1 : amount - 1
            E_new = E_new + dist_matrix(sol_new(i), sol_new(i + 1));
        end
        % 再算上从最后一个城市到第一个城市的距离
        E_new = E_new + dist_matrix(sol_new(amount), sol_new(1));        
        if E_new < E_current
            E_current = E_new;
            sol_current = sol_new;
            if E_new < E_best
                % 把冷却过程中最好的解保存下来
                E_best = E_new;
                sol_best = sol_new;
            end
        else
            % 若新解的目标函数值大于当前解的，则仅以一定概率接受新解
            if rand < exp(-(E_new - E_current)/t)
                E_current = E_new;
                sol_current = sol_new;
            else
                sol_new = sol_current;
            end
        end
    end
    t = t * ratio;		% 降温
end
disp(['最优解为：', num2str(sol_best)]);
disp(['最短距离：', num2str(E_best)]);
x_path = [coordinates(sol_best, 1); coordinates(sol_best(1), 1)];
y_path = [coordinates(sol_best, 2); coordinates(sol_best(1), 2)];
plot(x_path, y_path, 'LineWidth', 2)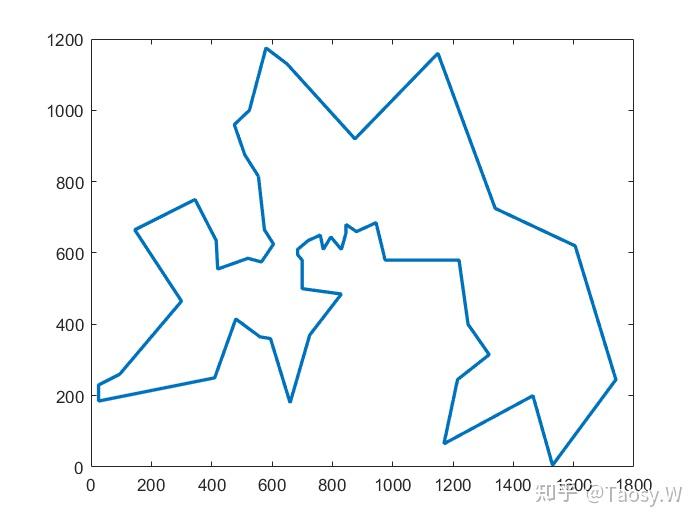

算法下载：

SSA: Salp Swarm Algorithm

clear;clc;
% 搜索数量
SearchAgents_no = 30;
% 最大迭代次数
Max_iter = 200;
% 变量维度
dim = 2;
% 上限
ub = 10 * ones(1, dim);
% 下限
lb = -10 * ones(1, dim);
% 初始化位置
Positions = rand(SearchAgents_no, dim) .* repmat(ub - lb, SearchAgents_no, 1) + repmat(lb, SearchAgents_no, 1); 
Convergence_curve = zeros(1, Max_iter);
SalpFitness = nan(1, Max_iter);
Sorted_salps = nan(SearchAgents_no, dim);
% 计算适应度值
for i = 1 : SearchAgents_no
    SalpFitness(1, i) = ObjFun(Positions(i, :));
end
[sorted_salps_fitness, sorted_indexes] = sort(SalpFitness);
for i = 1:SearchAgents_no
    Sorted_salps(i, :) = Positions(sorted_indexes(i), :);
end
FoodPosition = Sorted_salps(1, :);
FoodFitness = sorted_salps_fitness(1);
Convergence_curve(1) = FoodFitness;
% 主循环
for l = 2:Max_iter
    c1 = 2*exp(-(4*l/Max_iter)^2);    
    for i = 1:SearchAgents_no
        SalpPositions = Positions';      
        if i <= SearchAgents_no/2
            for j = 1:dim
                c2 = rand();
                c3 = rand();
                if c3 < 0.5 
                    SalpPositions(j, i) = FoodPosition(j) + c1*((ub(j) - lb(j))*c2 + lb(j));
                else
                    SalpPositions(j, i) = FoodPosition(j) - c1*((ub(j) - lb(j))*c2 + lb(j));
                end
            end  
        elseif i > SearchAgents_no/2
            point1 = SalpPositions(: , i-1);
            point2 = SalpPositions(: , i);
            SalpPositions(:, i) = (point2 + point1) / 2;
        end
        Positions= SalpPositions';
    end
    % 更新
    for i = 1:SearchAgents_no
        % 边界处理：越界赋值为边界值
        Flag4ub = Positions(i, :) > ub;
        Flag4lb = Positions(i, :) < lb;
        Positions(i, :) = (Positions(i, :).*(~(Flag4ub + Flag4lb))) + ub.*Flag4ub + lb.*Flag4lb;        
        SalpFitness(i) = ObjFun(Positions(i, :));
        if SalpFitness(i) < FoodFitness
            FoodPosition = Positions(i, :);
            FoodFitness = SalpFitness(i);
        end
    end    
    Convergence_curve(l) = FoodFitness;
end
disp(['最优值：' num2str(FoodPosition)]);
disp(['最优值对应目标函数：' num2str(FoodFitness)]);
subplot(1, 2, 1)
plot(Convergence_curve, 'LineWidth', 2);
xlabel('迭代次数');
ylabel('适应度值');
title('适应度曲线');
len = 50;
xRange = linspace(lb(1), ub(1), len);
yRange = linspace(lb(2), ub(2), len);
[xMap, yMap] = meshgrid(xRange, yRange);
zMap = zeros(len);
for i = 1 : len
    for j = 1 : len
        zMap(i, j) = ObjFun([xMap(i, j), yMap(i, j)]);
    end
end
subplot(1, 2, 2)
surf(xRange, yRange, zMap);
view(-45, -45);
shading interp
hold on
plot3(FoodPosition(1), FoodPosition(2), FoodFitness, 'o', 'MarkerFaceColor', 'r', 'MarkerSize', 10);
hold off
set(gcf, 'Position', [400, 200, 900, 400]);

function result = ObjFun(x)
x1 = x(1);
x2 = x(2);
t = x1^2 + x2^2;
result = 0.5 + (sin(sqrt(t))^2 - 0.5) / (1 + 0.001 * t)^2;
end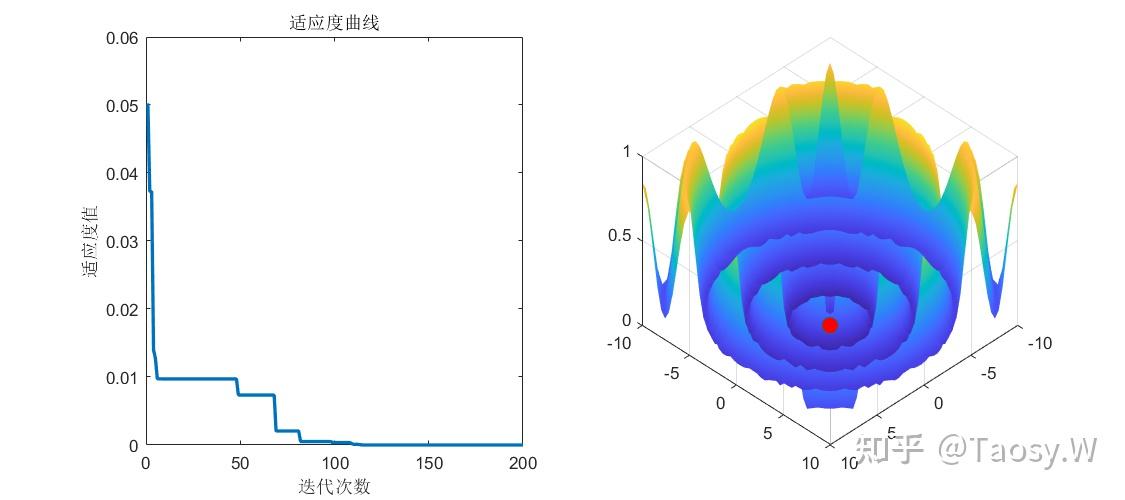

https://zhuanlan.zhihu.com/p/417554029 https://zhuanlan.zhihu.com/p/417554029

算法下载：

https://au.mathworks.com/matlabcentral/fileexchange/55667-the-whale-optimization-algorithm

The Whale Optimization Algorithm

clear;clc;
% 鲸鱼数量
SearchAgents_no = 30;
% 最大迭代次数
Max_iter = 200;
% 变量维度
dim = 2;
% 上限
ub = 10 * ones(1, dim);
% 下限
lb = -10 * ones(1, dim);
%%%%% 初始化
Leader_pos = zeros(1, dim);
Leader_score = inf;
% 初始化位置
Positions = rand(SearchAgents_no, dim) .* repmat(ub - lb, SearchAgents_no, 1) + repmat(lb, SearchAgents_no, 1); 
Convergence_curve = zeros(1, Max_iter);
% 主循环
for t = 1:Max_iter
    for i = 1:SearchAgents_no
        % 边界处理：越界赋值为边界值
        Flag4ub = Positions(i, :) > ub;
        Flag4lb = Positions(i, :) < lb;
        Positions(i, :) = (Positions(i, :).*(~(Flag4ub + Flag4lb))) + ub.*Flag4ub + lb.*Flag4lb;
        % 计算目标函数
        fitness = ObjFun(Positions(i, :));
        % 更新领头位置
        if fitness < Leader_score
            Leader_score = fitness;
            Leader_pos = Positions(i, :);
        end
    end
    % 线性递减
    a = 2 - t * 2 / Max_iter;
    a2 = -1 - t / Max_iter;   
    % 更新位置
    for i = 1 : SearchAgents_no
        r1 = rand();
        r2 = rand();
        A = 2*a*r1 - a;
        C = 2*r2;
        b = 1;
        l = (a2-1)*rand+1;
        p = rand();
        for j = 1 : dim 
            if p < 0.5   
                if abs(A) >= 1
                    rand_leader_index = floor(SearchAgents_no*rand() + 1);
                    X_rand = Positions(rand_leader_index, :);
                    D_X_rand = abs(C*X_rand(j) - Positions(i, j));
                    Positions(i, j) = X_rand(j) - A*D_X_rand;
                    
                elseif abs(A) < 1
                    D_Leader = abs(C*Leader_pos(j) - Positions(i, j));
                    Positions(i, j) = Leader_pos(j) - A*D_Leader;
                end
            else
                distance2Leader = abs(Leader_pos(j) - Positions(i, j));
                Positions(i, j) = distance2Leader*exp(b.*l).*cos(l.*2*pi) + Leader_pos(j);
            end
        end
    end
    Convergence_curve(t) = Leader_score;
end
disp(['最优值：' num2str(Leader_pos)]);
disp(['最优值对应目标函数：' num2str(Leader_score)]);
subplot(1, 2, 1)
plot(Convergence_curve, 'LineWidth', 2);
xlabel('迭代次数');
ylabel('适应度值');
title('适应度曲线');
len = 50;
xRange = linspace(lb(1), ub(1), len);
yRange = linspace(lb(2), ub(2), len);
[xMap, yMap] = meshgrid(xRange, yRange);
zMap = zeros(len);
for i = 1 : len
    for j = 1 : len
        zMap(i, j) = ObjFun([xMap(i, j), yMap(i, j)]);
    end
end
subplot(1, 2, 2)
surf(xRange, yRange, zMap);
view(-45, -45);
shading interp
hold on
plot3(Leader_pos(1), Leader_pos(2), Leader_score, 'o', 'MarkerFaceColor', 'r', 'MarkerSize', 10);
hold off
set(gcf, 'Position', [400, 200, 900, 400]);

function result = ObjFun(x)
x1 = x(1);
x2 = x(2);
t = x1^2 + x2^2;
result = 0.5 + (sin(sqrt(t))^2 - 0.5) / (1 + 0.001 * t)^2;
end

上一篇 : ——基于当代西方环境美学视域——基于当代西方环境美学视域

下一篇 : 关于深入推进优质粮食工程的意见

【返回列表】